Teste de Normalidade e Homogeneidade

Antes de realizar análises estatísticas, é importante verificar se os dados atendem a certas premissas para garantir resultados confiáveis. Entre essas premissas estão a normalidade e a homogeneidade de variâncias. O teste de normalidade verifica se os dados seguem uma distribuição normal, sendo esta uma suposição necessária em muitos testes paramétricos, como o teste t. Para avaliar a normalidade, podem ser utilizados testes como Shapiro-Wilk e Anderson-Darling além da inspecção visual por histogramas e gráficos Q-Q plot. Outro aspecto importante é verificar a homogeneidade de variâncias, que consiste em avaliar se os grupos possuem variâncias semelhantes. Essa condição é essencial para o uso correto do teste t padrão. Se as variâncias forem diferentes entre os grupos, pode-se utilizar o teste t de Welch, que é apropriado para situações com variâncias heterogêneas. Para verificar a homogeneidade de variâncias, é comum utilizar o teste de Levene, que é robusto mesmo quando os dados não seguem uma distribuição normal, e o teste de Bartlett, que é indicado quando os dados são normalmente distribuídos. Visualizações como boxplots também ajudam a identificar diferenças nas variâncias entre os grupos.

Realizar os testes de normalidade e homogeneidade de variâncias antes de prosseguir com análises estatísticas garante a confiabilidade das conclusões e evita interpretações equivocadas dos dados analisados.

library(car) # Funções de análise estatística avançadas (ANOVA, testes de homogeneidade).

Shapiro-Wilk

Testa normalidade dos dados.

shapiro.test(dat_mg2$Mg2)

    Shapiro-Wilk normality test

data:  dat_mg2$Mg2
W = 0.97269, p-value = 0.9146

  • p-value = 0.9146 → muito maior que 0.05

  • Não rejeitamos H₀, ou seja, os dados de Mg2 podem ser considerados normalmente distribuídos.

shapiro.test(dat_mg2$control)

    Shapiro-Wilk normality test

data:  dat_mg2$control
W = 0.93886, p-value = 0.5404

  • p-value = 0.5404 → também maior que 0.05

  • Os dados de control também seguem uma distribuição normal.

Histogramas

Visualização da distribuição.

hist(dat_mg2$Mg2, main = "Histograma de Mg2", xlab = "Valores de comp")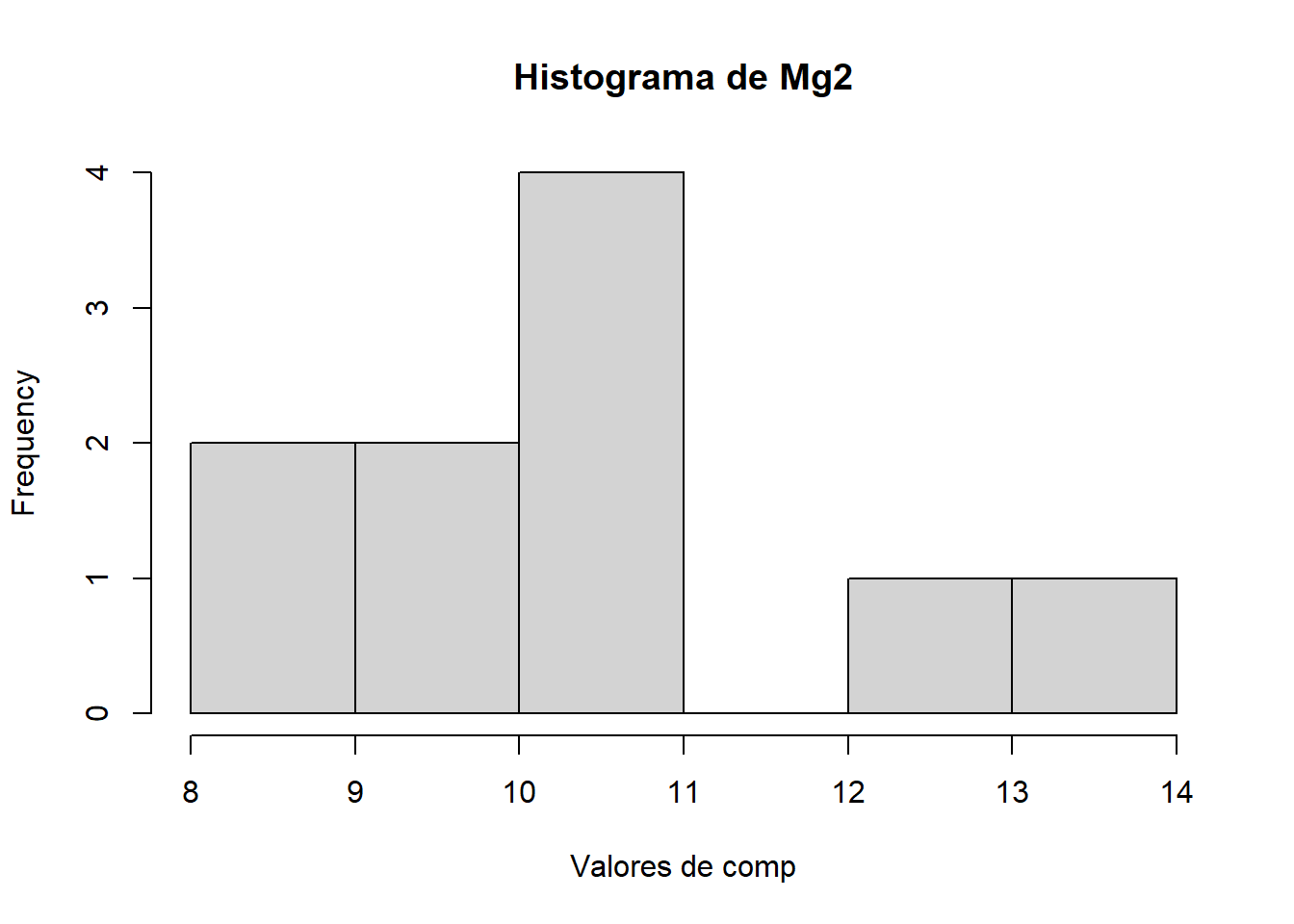

hist(dat_mg2$control, main = "Histograma de Controle", xlab = "Valores de comp")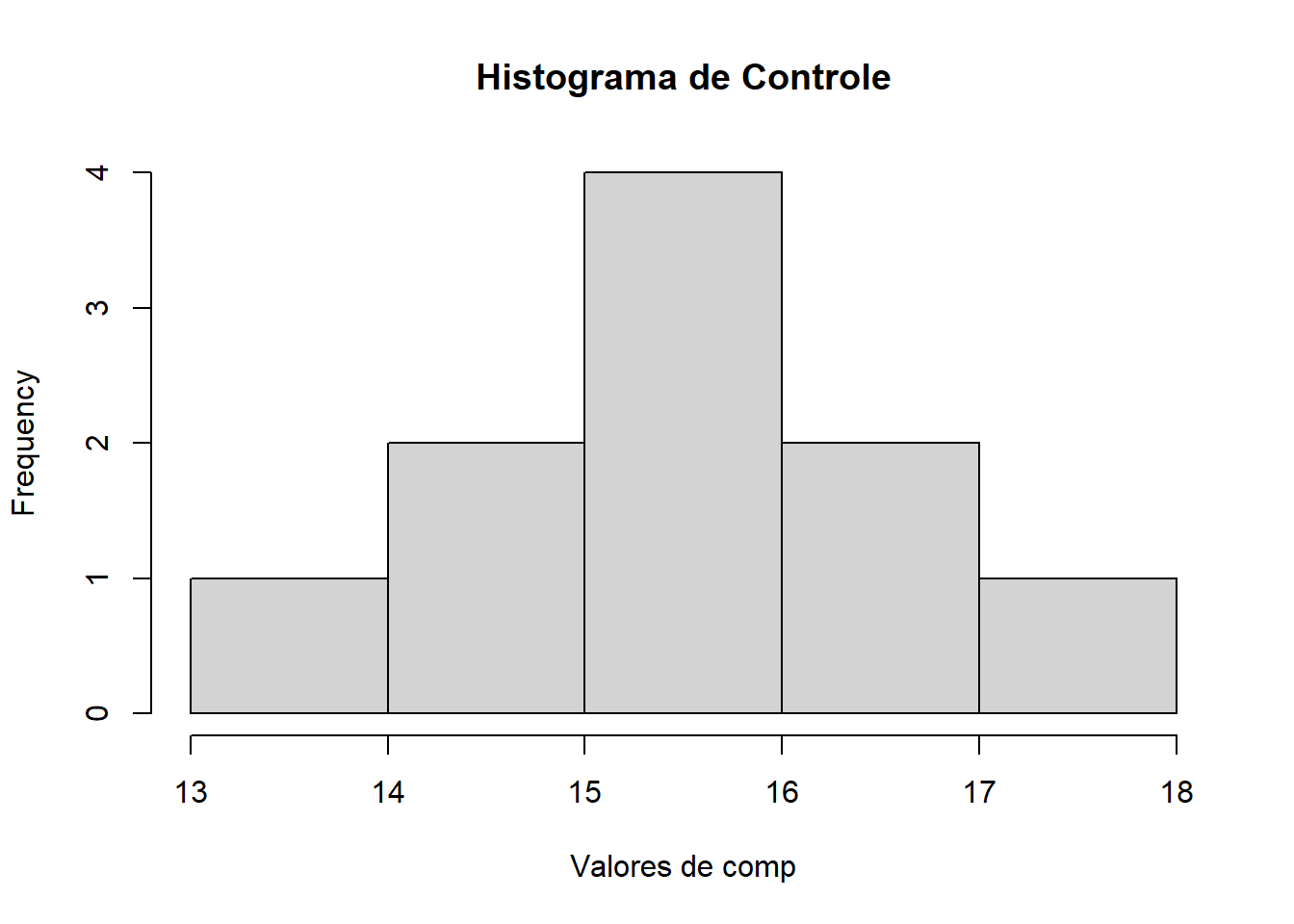

Gráficos Q-Q plot

Gráfico Q-Q (quantil-quantil) dos resíduos, que ajuda a visualizar se eles seguem uma distribuição normal.

qqnorm(residuals(m2))
qqline(residuals(m2))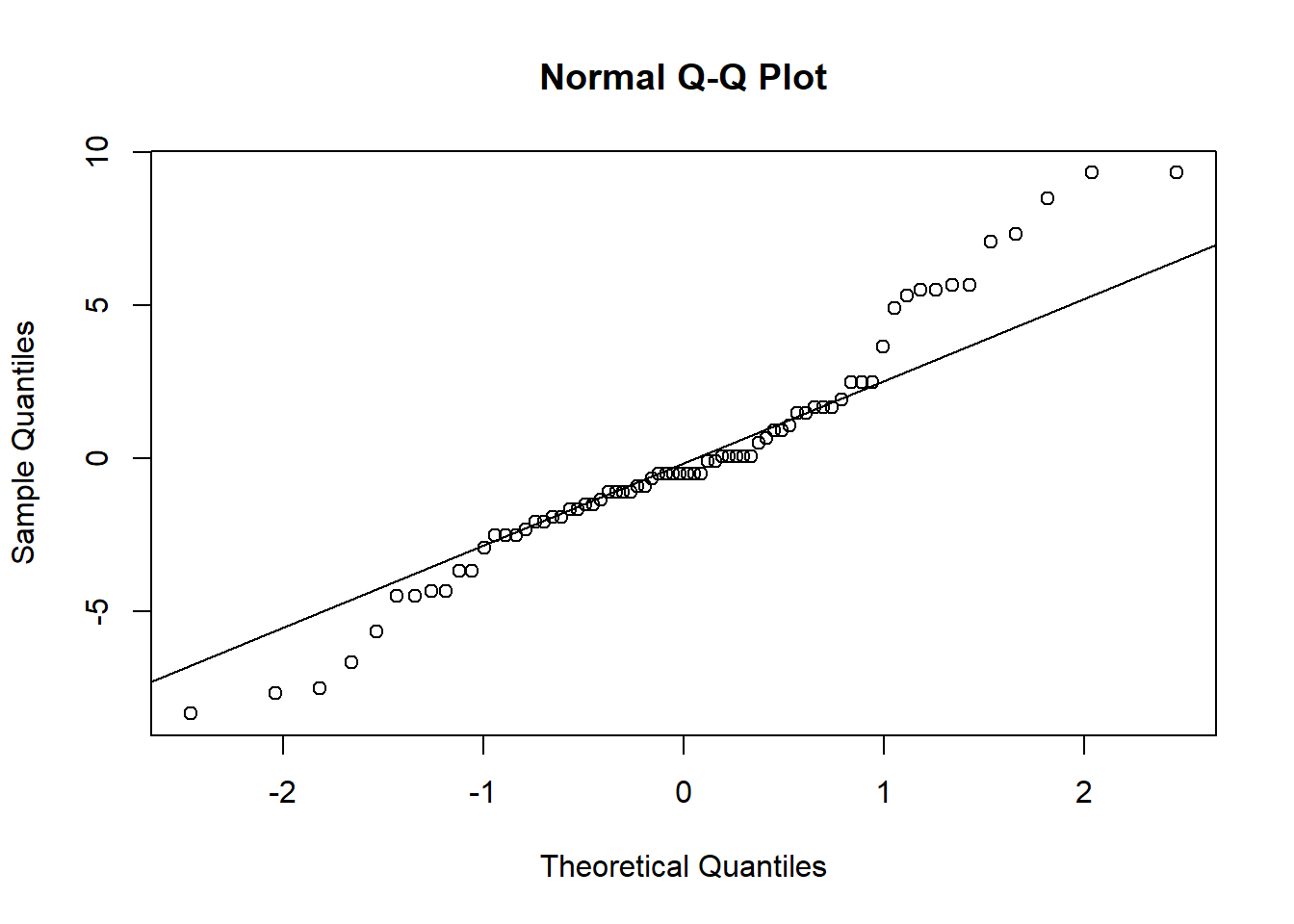

Teste F

Testar a homogeneidade de variânciascoms de dois grupos apenas.

var.test(dat_mg2$Mg2, dat_mg2$control)

    F test to compare two variances

data:  dat_mg2$Mg2 and dat_mg2$control
F = 1.4781, num df = 9, denom df = 9, p-value = 0.5698
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.3671417 5.9508644
sample estimates:
ratio of variances 
          1.478111
  • Esses testes verificam as premissas do teste t.

Teste de Barttlet

Também testa a homogeneidade de variâncias de dois ou mais grupos.

bartlett.test(count ~ spray, data = insetos)

    Bartlett test of homogeneity of variances

data:  count by spray
Bartlett's K-squared = 25.96, df = 5, p-value = 9.085e-05

  • Bartlett’s K-squared = 25.96: é o valor estatístico do teste.

  • df = 5: são os graus de liberdade (número de grupos − 1, no caso, 6 sprays).

  • p-value = 9.085e-05 (ou 0.00009085): é muito menor que 0.05.

p-valor é muito pequeno, rejeitamos a hipótese nula (H₀). Isso significa que as variâncias entre os grupos são significativamente diferentes.